You are here: wiki.doebe.li>Informatik_ Web>ProblemloeseArgument (08 Feb 2015, BeatDoebeli)EditAttach

Problemlöseargument

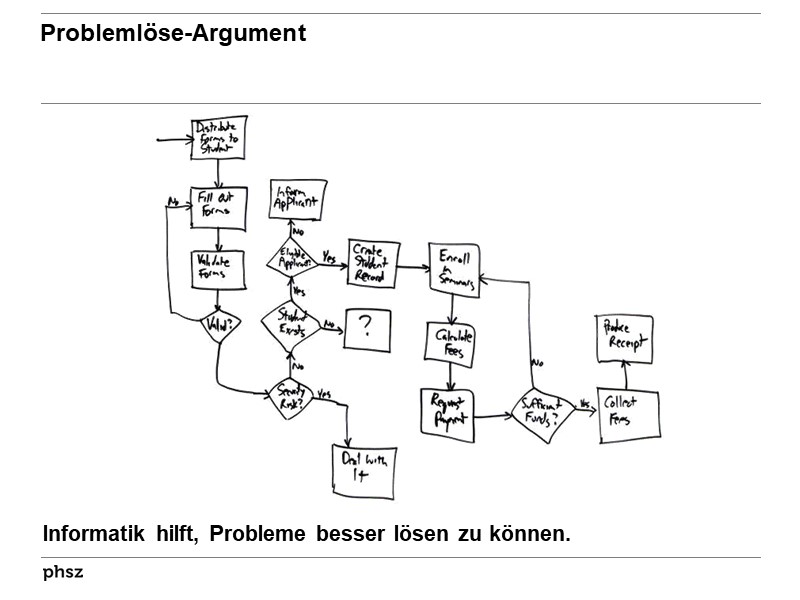
img043.jpg

Formulierung des Arguments

Grundkonzepte der Informatik sind hilfreich beim analytischen Denken und Lösen von Problemen über die Informatik hinaus.

Erklärung des Arguments

Informatik als Denkwerkzeug hat nicht nur im Bildungs- und Wissenschaftsbereich etwas zu bieten. Das Problemlöseargument (Biblionetz:a1052) zielt auf den Alltag: Informatik stellt Werkzeuge und Verfahren zur Verfügung, wie sich auch im Alltag Probleme strukturiert beschreiben, diskutieren und damit besser lösen lassen – auch ohne den Einsatz von Computern. So können zum Beispiel Flussdiagramme helfen, Abläufe zu verstehen und zu optimieren, unterschiedliche Datenstrukturen wie Listen, Tabellen, Bäume und Graphen unterstützen das problemgerechte Erfassen, Verarbeiten und Darstellen von Daten, und Visualisierungstechniken wie Conceptmaps helfen beim Nachdenken über Strukturen und Zusammenhänge. Bei der Beschäftigung mit Informatik lernt man diese Werkzeuge kennen und schult auch das entsprechende Denken. Viele dieser Konzepte und Werkzeuge existieren nicht erst seit der Entstehung der Wissenschaft Informatik. Doch erst die Informatik macht den Umgang mit solchen Werkzeugen explizit zum Thema. Guter Informatikunterricht fördert daher nicht nur die Nutzung solcher Konzepte und Werkzeuge, sondern hilft Schülerinnen und Schülern auch, künftig selbst die geeigneten Denkwerkzeuge zu finden. So bietet sich Informatik an, über Problemlöseheuristiken oder den Unterschied zwischen Korrektheit und Viabilität (Biblionetz:w00170) nachzudenken.

Quelle: Beat Döbeli Honegger (2015). Mehr als 0 und 1 (Biblionetz:b06000)

Diskussion der Formulierung des Arguments

fasel

Inhaltliche Diskussion des Arguments

  • Gibt es bereits Studien, ob Informatikunterricht die Problemlösefähigkeit von Lernenden fördert? Man muss vorsichtig sein mit der Behauptung, die in der Informatik erworbenen Kompetenzen liessen sich auf andere Gebiete übertragen. Ich glaub im Falle von Latein scheint dieser Nachweis nicht gelungen zu sein. Wer weiss dazu mehr? -- BeatDoebeli - 11 Sep 2009
    • Ist das wirklich zentral? Mathematik und Physik werden ja auch unterrichtet, ohne dass sie den Nachweis erbringen müssen, nützlich zu sein. Von Latein wurde der Nachweis "verlangt", weil niemand (sorry an alle Lateinlehrpersonen) den Sinn des Lateinunterrichts mehr sah; in der Informatik sind die Verhältnisse anders gelagert: Im Kanton Bern soll "Informatik" (ProblemSchwammigerBegriff) ja bereits auf Primarstufe unterrichtet werden. Abgesehen davon scheint mir der Nutzen für die Problemlösungskompetenzen bei Prozess- und Strukturfragen sonnenklar; Beispiele dazu wären aber nett. -- PascalSchuppli - 15 Sep 2009
      • Sonnenklar, ja. Aber warum braucht es dazu Informatik? Zusammenhänge werden auch im Politik/Wirtschaftsunterricht deutlich gemacht. Algorithmisches Denken macht die Mathematik. -- TorstenOtto - 18 Sep 2009 (advocatus diaboli)
        • Also ich habe in der Mathematik nie algorithmisch gedacht, leider. frown, sad smile Aber letztlich wäre ja egal, in welchem Fach das gemacht wird, solange es die gleichen Konzepte sind. -- PascalSchuppli - 22 Sep 2009

Erfasste Literaturerwähnungen im Biblionetz

Edit | Attach | Print version | History: r8 < r7 < r6 < r5 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r8 - 08 Feb 2015, BeatDoebeli
 
This site is powered by FoswikiCopyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Seite genereriert um 04 Nov 2024 - 23:16
Ideas, requests, problems regarding wiki.doebe.li? Send feedback